La maravillosa transformación
Serie-Paralelo
Ultima modificación (estilo) 2011-03-06
Por Miguel R. Ghezzi (LU 6ETJ)
www.solred.com.ar/lu6etj
SOLVEGJ Comunicaciones
Una de las áreas más "complicadas" para el radioaficionado
Novicio es la asociada con las adaptaciones de impedancia; área que abarca
cuestiones tales como el
Pi de nuestro viejo trasmisor a válvulas, el transmatch, la adaptación entre las etapas de los
amplificadores y se vincula con el "Hairpin" de nuestra direccional...
Así como las leyes de Ohm y de Kirchhoff, junto con el teorema de
Thevenin y Norton permiten resolver fácilmente una red o malla, si podemos
comprender la simple transformación Serie - Paralelo podremos resolver muchas
situaciones habituales en la radio.
Observe los dos circuitos de la fig. 1, son
levemente diferentes. Con un instrumento adecuado podríamos medir la impedancia
de cada uno, vista desde los terminales del generador EAC. Ahora bien ¿sería posible darles a cada uno de ellos algún valor
de R y de X tal que
ambos dieran la misma lectura de Impedancia? La respuesta es SI...
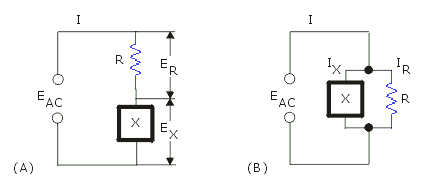
Esto quiere decir que el circuito de la fig. A
tendría un homólogo en el de la B. Vemos que uno está constituido por dos elementos en serie
mientras que
el otro lo está por dos elementos en paralelo y que, puesto que ambos
tienen la misma impedancia, estos dos circuitos son equivalentes.
Haremos una salvedad: sabemos que la Impedancia de un circuito (a menos que sea puramente resistivo)
en general depende de la frecuencia, por ende al encontrar valores de R y X
tales que la impedancia de ambos circuitos es la misma para realizar la medición de
impedancia, esta medición debe hacerse en una frecuencia única. Si cambiáramos la frecuencia de
medición encontraríamos que ambos circuitos ya no tienen la
misma impedancia, y dejan de ser homólogos, de manera que los circuitos A y B son equivalentes
pero en una
sola frecuencia. en otra frecuencia diferente también habrá un
homólogo de cualquiera de ellos pero con diferentes valores, de R y X
Lo interesante es que con un par de fórmulas siempre podremos convertir
rápidamente un
circuito como el de la fig. A en uno como el de la fig. B y viceversa y esto nos será muy útil para comprender el funcionamiento de numerosos circuitos de
adaptación de impedancias.
Si conocemos los valores de un circuito serie y queremos averiguar los
valores equivalentes en paralelo empleamos las siguientes igualdades, los
sufijos "p" y "s" representan paralelo y serie respectivamente:
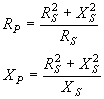 |
Para obtener el equivalente
paralelo de dos elementos en serie. |
Si conocemos los valores de un circuito paralelo y queremos averiguar los
valores equivalentes en serie empleamos estas otras:
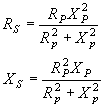 |
Para obtener el equivalente
serie de dos elementos en paralelo. |
Un caso práctico:
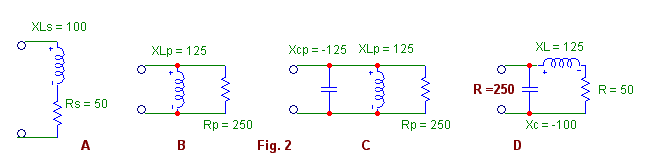
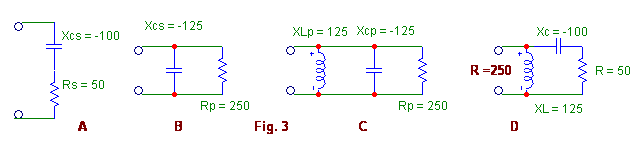
El circuito de la fig. 2A contiene una
resistencia que "casualmente" es 50 Ohms en serie con una
reactancia inductiva de 100 Ohms. Si aplicamos la fórmula se
convertirá en el circuito paralelo de la fig 2B. Ahora, nuestro circuito
equivalente tiene una resistencia de 250 Ohms en paralelo con una reactancia inductiva de
+125 Ohms.
Ahora bien fíjese que interesante: ¿Qué sucedería si a este circuito
resultante le
conectáramos en paralelo un capacitor cuya reactancia también fuera de 125
Ohms pero negativos, es decir capacitiva?. Ambas reactancias, como sabemos, se
cancelarán y solo será "visible" la resistencia de 250 Ohms.
Note que la el inductor en la fig 2-D permanece físicamente en serie, dado que
los de la figuras B y C son únicamente sus "equivalentes".
¿Se advierte lo que hemos logrado al instalar el inductor y el capacitor en esa
disposición? ¡Conseguimos convertir la resistencia de 50
Ohms en una de 250 Ohms...!
Esta red de adaptación, una de las más simples,
es la popular red
"L". Tiene una gran capacidad de adaptación, por ejemplo, si
cambiáramos el valor de la inductancia serie de 100 a 500 Ohms, la resistencia
equivalente paralelo que obtendríamos estaría en el orden de los 5000 Ohms,
con ella podríamos muy fácilmente adaptar un dipolo de media onda alimentado
al extremo a una línea de 50 Ohms.
Veamos ahora qué sucede si a la resistencia de 50 Ohms le conectamos en
serie un capacitor cuya reactancia sea de -100 Ohms (es decir igual que la
reactancia del ejemplo anterior, pero esta vez capacitiva). Realizando las
cuentas vemos que ahora tendremos un circuito equivalente paralelo formado esta
vez un
capacitor y una resistencia. Cancelando la reactancia equivalente capacitiva con
una inductiva de igual valor nuevamente obtenemos una adaptación. También es
una red "L", solo que en este caso el elemento en serie es un
capacitor y el elemento en derivación un inductor.
¿Cuál es la diferencia entre ellas?
Una diferencia importante es que la red "L" con inductancia en
serie y capacidad en derivación tiene características de filtro pasabajos;
esto nos favorece si deseamos que la red adaptadora ayude a cancelar
armónicos. Por el contrario la que tiene como elemento serie el capacitor y
como elemento en derivación el inductor, tiene características de filtro
pasaaltos, que también podemos aprovechar para ayudar a evitar que ingresen
a un receptor señales de la banda de broadcasting cuando se opera en 160 u
80m.
Observe también que no importa si el componente
es un inductor o un capacitor, estando en serie su efecto es el de aumentar la
resistencia equivalente. La conexión de un componente en serie producirá siempre
un efecto "elevador" de resistencia.
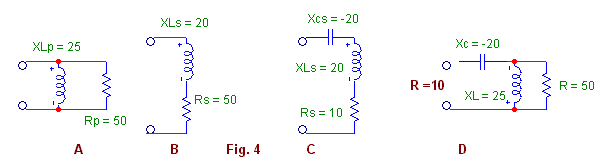
En efecto, si aplicamos el segundo juego de
fórmulas vemos que el circuito equivalente serie para este circuito ofrece
una resistencia equivalente menor. (10 ohms) y otro detalle a tener en cuenta es
que para cancelar la reactancia inductiva equivalente, ahora habrá que
intercalar un capacitor en serie, como se observa en las figuras C y D.
Aplicaciones comunes en la
radio
La primera que nos viene a la mente es justamente un transmatch,
también el
circuito de adaptación interetapa de un amplificador de RF. Una interesante
aplicación no tan evidente cuando la vemos en una antena, es la conocida como "Beta Match"
que emplea un alambre en forma de U o bobina llamado "hairpin" (hebilla).
Veamos: normalmente una antena direccional Yagi de varios elementos posee una impedancia
en el irradiante menor de 50 Ohms y usualmente resultará conveniente
adaptarla a la línea de trasmisión, que en nuestro ámbito muy probablemente será
una 50 Ohms.
Hairpin o Beta Match
Según vimos en el ejemplo de la figura
3-A, si conectamos en serie con una
resistencia dada un capacitor, la resistencia equivalente paralelo aumenta y que
la
reactancia equivalente capacitiva paralela que posibilitó la transformación
puede cancelarse mediante un inductor lográndose la adaptación buscada.
Aplicando esta noción a nuestro problema, vemos que:
Si hacemos que el irradiante tenga una longitud
menor que la necesaria para su autorresonancia, el presentará una componente capacitiva en su punto de alimentación,
produciendo con este ardid una situación similar a la de la figura 3-A y
haciendo este acortamiento tal que la reactancia capacitiva que presente el
irradiante sea la justa para que el equivalente paralelo
tenga una resistencia de 50 Ohms conseguimos el efecto buscado, no queda
solamente cancelar la reactancia capacitiva paralela resultante con un
inductor para finalizar nuestra adaptación. El
hairpin no es otra cosa que ese inductor -conectado en derivación- para
lograr la cancelación buscada. El método del hairpin, no es otra cosa que una
adaptación tradicional en "L"
Copyright © 2004 - 2014
Miguel Ricardo Ghezzi - LU 6ETJ - Argentina.
Volver a la página
principal